
So you've got a couple of options when you're trying to calculate the area of a rhombus. For triangle 1, in centimeters, thats 36 x 21.6 / 2 388.8 square centimeters. The area of each triangle is its width times its height, divided by two. So, this formula of d1 times d2 divided by 2 has to apply. From the diagram, you can see that the template shape contains three triangles. The other way, is to say well, the diagonals of a rhombus are also perpendicular and they bisect each other. The first way is to say if you know a height and a corresponding base, then you can just calculate the area as base times height. So there's going to be 2 ways for you to calculate the area of a rhombus. The key thing to realizing this formula, was cutting out these pieces, rotating and translating and saying that the diagonals of a kite, that this diagonal is bisected by the other diagonal.

So another way of writing this is to realise that d2 and d1 are in your numerator, so you just rearrange it and write it as d2 times d1 divided by 2. So the area of this rectangle, our base is d2 divided by 2 times our height which is d1. So now we've created since we know that these are all right angles, we have created a rectangle, and we know that the area of a rectangle is the base times the corresponding height. Theorem The area of a kite equals half the product of its diagonals. This means the kite can be divided into 2 isosceles triangles with a common baseso its area will equal the sum of the areas of the two. The longer diagonal bisects the shorter diagonal. Which means this piece right here is going to be d2 divided in half. In a kite, the diagonals are perpendicular. What else do we know about the diagonals of a kite? Well, I know that this d2 is bisected by the other diagonal. Area Of A Kite Displaying top 8 worksheets found for - Area Of A Kite. Use this worksheet to practice finding area of a kite. So let's start off by saying well, what do we know? We know that this distance right here is the distance of diagonal 1. This set of area of a kite worksheets for 7th grade and 8th grade students specifies the lengths of the diagonals in varied units. So now we have this other piece here that we cut out and up here we have another piece that we cut out. But then I said I translate it and rotate it. So I'm going to redraw my kite, where we have our initial piece which is right here and we have this bottom piece right here. So I'm going to do the same thing with this piece right here. I'm going to do the the same thing with this piece except and actually by translate I meant translate and then rotate. So what I'm going to do is I'm going to cut out this piece right here out of the white board and I'm going to translate it until it fits into this area right here. We know that the diagonals in the kite are perpendicular. So is there any way that we can take this kite and rearrange its pieces to make a rectangle. We know this area is going to be equal to its base times its corresponding height. We know that the area of a rectangle, so if I write in some right angles, label these as parallel.
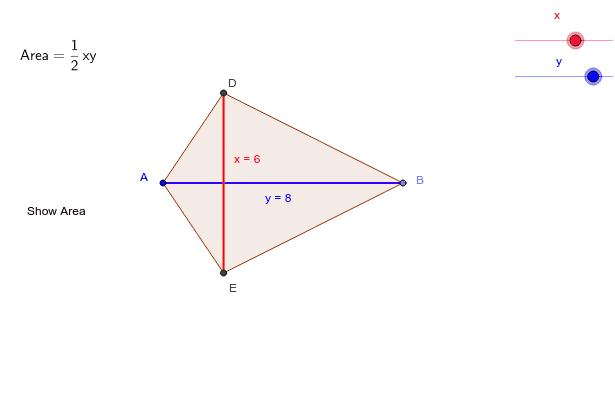
These types of geometric figures are referred to as composite figures.What is the area of a kite where all you know is the length of each of those diagonals? Well, let's go back to what we do know. If needed, draw a picture of the kite on the coordinate plane. Many geometric figures are made up of two or more common figures, and their areas can be calculated using a combination of the area formulas above. The area of an ellipse with semi-major axis, a, and semi-minor axis, b, is: Problem Set B 4 Find the area of the kite shown. The area of a regular octagon with side length s is: kite i 12 24 20 16 300 16 Part Three: Problem Sets Problem Set A 1 Find the area of a kite with diagonals 6 and 20. The area of a regular pentagon with side length s is: The area of a regular hexagon with side length s is: The area of a kite, or rhombus, with diagonal length d 1 and d 2 is: The area of a trapezoid with bases, b 1 and b 2, and height, h, is: The area of a parallelogram with base, b, and height, h, is: The area of a rectangle with length, l, and width, w, is: The area of an equilateral triangle with side length, s, is: Where a, b, and c are side lengths, and Equilateral triangle If the side lengths of the triangle are given, the area can be found using: The area of a triangle with base, b, and height, h, is: The exact area of many common shapes can be calculated using well-defined formulas.
#AREA OF A KITE HOW TO#
The area of a two dimensional shape or geometric figure is the space contained within its perimeter. how to find area of a kite when the diagonals are not givenO-level Additional Mathematics Challenging Drill Questions. Home / geometry / area and perimeter / area formula Area formula


 0 kommentar(er)
0 kommentar(er)
